Why are assigning students to public schools and organ donation economics? So ask many people. Although it is cliché, the simple answer is in the definition of economics:

“Economics is a science which studies human behavior as a relationship between ends and scarce means which have alternative uses.” -- Lionel Robbins

No doubt that seats at public schools and organs are scarce, but what is “non-economics” here is that there is no price or monetary transfer involved – public schools are free, and laws usually forbid paying organ donors. This is exactly what makes unique Al Roth’s studies in market design.

The goal of market design is to achieve efficient outcomes: Students should be assigned to the schools that they prefer; patients who need an organ transplant should receive a donated organ in time. In a traditional market, this goal can be achieved with the help of a price system. If a student likes a school more, she is willing to pay a higher price, so is a patient in a greater need of an organ transplant. In real life, however, for various reasons, there are many occasions when price or monetary transfer is either forbidden or very limited. The case with the lack of or limited use of monetary transfer is described by the economic term, non-transferable utility. Other examples include allocating doctors to hospitals, housing/dormitory allocation on campus, office allocation, and course allocation.

1. Matching and Stability

In the above examples, there are two sides of agents – courses and students, schools and students, or organ donors and patients – whom we want to match together. Note that neither side can be divided into pieces: A seat in a course or a school cannot be shared by two students; neither can a kidney be shared by multiple patients. Hence agents on each side have indivisibility, and yet they are heterogeneous. Otherwise, if all agents are the same, there is little room to have better allocations.

One may have notice that we have been mixing two different scenarios. In office/housing/course allocation, office/housing/course does not make active decisions or does not rank agents on the other side. This is so called one-sided matching which includes the everyday product market. The product itself does not care about who its owner is.

There is yet another very different setting, two-sided matching, where both sides make active decisions and rank the opposite side. Hospitals care which doctors they can hire, while doctors have preferences over hospitals; schools rank students; and both men and women actively select whom they marry.

In addition to non-transferable utility, this area of research assumes agents are rational such that they know their best interests and behave accordingly. After participating in a matching procedure, or a matching mechanism, agents end up with some allocations where agents from two sides matched with someone from the opposite side.

The key concept in matching is stability. As we assume rational agents, a “good” allocation or matching outcome should be such that no agent has incentives to leave her current match. More formally, the allocation is stable if there is no single agent who can obtain any gains from leaving her current match either to stay unmatched or to form a new match with some agent from the opposite side who will be strictly better off in the new match.

2. One-Sided Matching

One-sided matching is common in real life. The markets for consumer products, such as TV, computers, and cars, are examples. These products are usually allocated to people based on a price system, or the competitive market mechanism. Whoever can pay the price of the product gets the product. According to the first fundamental theorem of welfare economics, the allocation of a competitive market is Pareto efficient. Namely, by switching to a new allocation, no one can be made better off without someone being made worse off. Therefore, the allocation is also stable. This may explain why the market mechanism prevails in real life.

One may wonder why we cannot always use the market mechanism in one-sided matching. In many case, it is exactly because we are not allowed to use a price system or monetary payments. For example, selling human organs or selling children is forbidden in almost all countries. This is what Roth (2007) describes as repugnancy, and many of his contributions are designing the market given repugnancy as a constraint.

A key solution in one-sided matching with non-transferable utility is the top-trading cycle algorithm (TTC). Consider a set of agents and a set of indivisible objects, say houses, without using side-payments. Each agent initially owns one house and each house cannot be shared. The basic idea is that we may repeatedly find a subset of agents who could all obtain their preferred houses by swapping among themselves.

More formally, the TTC works as follows:

Step 1: Each agent “points to” the owner of her favorite house. Since there are a finite number of agents, there is at least one cycle. Each agent in a cycle is assigned the house of the agent she points to and removed from the market with her assignment. If there is at least one remaining agent, proceed with the next step.

Step t: Each remaining agent points to the owner of her favorite house among the remaining ones. Every agent in a cycle is assigned the object of the agent she points to and removed from the market with her assignment. If there is at least one remaining agent, proceed with the next step.

Shapley and Scarf (1974) proved that the TTC algorithm, being attributed to David Gale, always produces a stable allocation. Abdulkadiroğlu and Sönmez (1999) later generalized the model to allow for the possibility that some agents do not initially own any objects, while some objects have no initial owner.

This model of one-sided matching may seem a bit too abstract, but Roth, Sönmez and Ünver (2004) notice that it can be extended to kidney exchange which is an important real-world situation.

Suppose that there are two imaginary figures in our world: François Hollande, who is in need of a kidney transplant, and his girlfriend, Valérie Trierweiler, who is willing to donate one of her kidneys to him. Unfortunately, as it usually happens in real world, the two’s blood types do not match, and therefore Trierweiler’s kidney cannot be used in Hollande’s body. In a competitive market, Hollande could just purchase a kidney if he could afford it, or if not, Trierweiler could sell one of her kidneys and use the money to buy a compatible one for Hollande. For various reasons, this kind of transaction is repugnant and cannot happen. This is then very similar to the house allocation problem, except that Hollande “owns” a house in which he is not able to live. More importantly, there are many patients in a situation like Hollande – it may not be difficult to find someone to give you a kidney, but you have to be very lucky to have a compatible donor.

The idea of TTC can then be used to improve the lives of patients in this case. The information of all patient-donor pairs as Hollande and Trierweiler can be gathered, and figuratively each pair points to a pair who is willing to donate a compatible kidney. Whenever we can find a cycle among these pairs, we may perform the transplant for the patients in the cycle. A simple example is illustrated below. Suppose that there is another incompatible patient-donor pair Nicolas Sarkozy - Carla Bruni. Each pair alone is in a desperate situation, but, luckily, the two pairs together can form a cycle and lives can be saved.

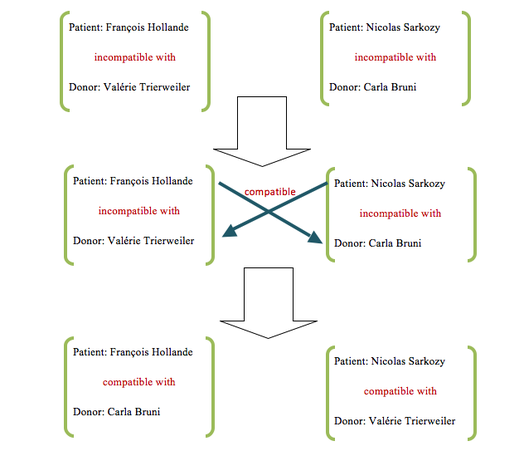
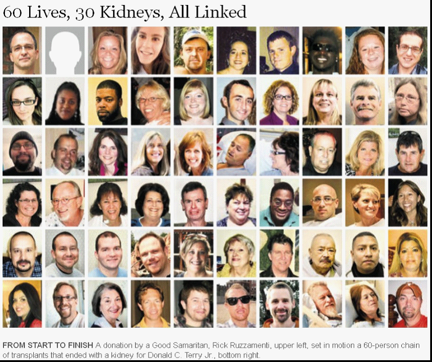
One important limitation of these cycles is that it is a small probability to find pairs among whom we can carry out the swapping. Bruni is willing to give Hollande her kidney only if Sarkozy is receiving a compatible kidney from Trierweiler – This happens rarely. Fortunately, there are also extremely generous people who are willing to donate their kidneys to anyone in need. In this case, as there are altruistic donors, we can form kidney exchange chains which make more transplants possible. For example, the following figure shows 30 transplants initiated by an altruistic donor.[1] Note that the last patient, Donald C. Terry Jr., bottom right, does not need to find a donor for the first donor, Rick Ruzzamenti, upper left, or for anyone.

Al Roth and his coauthors have been and still are working on issues related to human organ transplants.  One of the most important questions is to provide patients, donors, and also hospitals to participate in this kind of transplant chains. The thicker market is, i.e., the more people participate, the more chains can be formed. Certainly, the idea of the TTC algorithm can be applied to other cases of one-sided matching with non-transferable utility.

3. Two-sided matching

Two-sided matching is different in that both sides of agents make active decisions. College/university admission, school choice, and worker-firm match are common examples. Usually, worker-firm matching is considered in a transferable utility setting where firms face no restrictions when paying workers. It is therefore studied in another literature, search and matching theory, pioneered by Peter A. Diamond, Dale T. Mortensen, and Christopher A. Pissarides, the three Nobel laureates in 2010. In contrast, the tuition fees that public universities and public schools can charge students are highly regulated if not free. Therefore, a non-transferable utility setting is more appropriate.  

The most important mechanism in two-sided matching is the Gale-Shapley’s deferred acceptance mechanism (DA). It was introduced by Gale and Shapley in a model of marriage market where every man has a strict preference ranking over all women, and vice versa.

The DA can be set up in two alternative ways: either men propose to women, or women propose to men. In the latter case, the process begins with each woman proposing to the man she likes the best. Each man then looks at the different proposals he has received if any, retains what he regards as the most attractive proposal but defers from accepting it and rejects the others. The women who were rejected in the first round then propose to their second-best choices, while the men again keep their best offer and reject the rest. This continues until no women want to make any further proposals. As each of the men then accepts the proposal he holds, the process comes to an end.

First thing one has to remember is that the success of this mechanism in the marriage market has not been supported by scientific evidence. This may explain that there is no marriage market organized in this way.

Nonetheless, the DA mechanism has been proven very useful in many other settings. For example, when matching doctors with hospitals in the US, the National Resident Matching Program (NRMP) uses an algorithm which Roth (1984) found to be essentially equivalent to the employer-proposing DA mechanism.

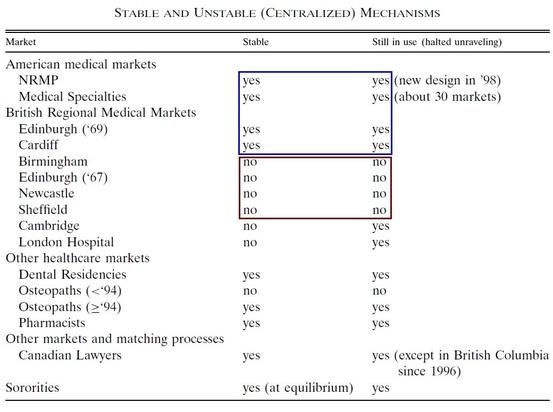
More importantly, recall that the key concept in matching is stability. Gale and Shapley theoretically prove that the DA mechanism always produces stable allocations. In a series of papers, Roth documents the evolution of the market for new doctors in the U.S. and in different regions in the U.K. and argues convincingly that a stable algorithm is the key of a functioning market. The following table from Roth (2002) highlights the importance of stability. There are only two cases where an unstable mechanism is still in use. These studies help us understand those markets better and have opened the door to Roth’s participation in actual design since 1990s.

Besides, the usefulness of the theory on market design has been further proven in the setting of school choice. In most urban areas in the US, students have the option to choose among the available public schools. Again, there is no price system and students and schools are heterogeneous. In Boston, New York City, and many other places, with the help from Roth and his coauthors, the mechanism used to allocate students to public schools has been reformed toward the DA or the TTC.

4. Market Design in Daily Life

Market design in the absence of price system, or with non-transferable utility, is still a growing field. Al Roth is still working on the design of markets for human organs, or more broadly the design of markets with repugnance. Besides, as society progresses, new challenges arise as well. For example, due to the increase in female labor force participation, more and more doctors jointly apply for positions as couples at hospitals. We need some new design in the DA mechanism to accommodate these new applications.

This need for market design is everywhere in daily life. In France, the AFFELNET system (Affectation des élèves par internet) is used in Paris and other cities to assign students from collége to lycées. It uses a version of school-proposing DA mechanism where students are allowed to rank 6 schools. In 2010 alone, the system allocated 16,500 students to 109 lycées in Paris. Another example is allocating M1 students to M2 programs at TSE. In all these cases, monetary payments are not used. The knowledge from Shapley, Roth, and other contributors in this field can help us better understand how these markets work and improve their function.

It is important to note that results from this field of research are by no means a substitute to the traditional market mechanism where the price system allocates resources. Instead, they are rather complementary, given repugnance is still prevalent in society. While we keep our fingers crossed for a competitive market, we can improve the market for public schools and organ donation even without a price system if the economist works as engineer.

【原文载于 Toulouse School of Economics 的学生杂志 TSEconomist 】

【原题：“Matching in Practice - A brief and incomplete introduction of Al Roth’s work” 】

何英华

新浪微博：@旁观组

team.bystanders@gmail.com

References and Further Readings:

Al Roth’s blog: http://marketdesigner.blogspot.com

Al Roth’s Webpage: http://www.stanford.edu/~alroth/or

http://kuznets.fas.harvard.edu/~aroth/alroth.html

Abdulkadiroglu, Atila and Tayfun Sonmez.1999. "House Allocation with Existing Tenants." Journal of Economic Theory, 88(2), 233-60.

Economic Sciences Prize Committee of the Royal Swedish Academy of Sciences, 2012, “Stable Allocations and the Practice of Market Design,” Scientific Background on the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2012.

Gale, David E. and Lloyd S. Shapley.1962. "College Admissions and the Stability of Marriage." American Mathematical Monthly, 69(1), 9-15.

Roth, Alvin E.1984. "The Evolution of the Labor Market for Medical Interns and Residents: A Case Study in Game Theory." The Journal of Political Economy, 92(6), 991-1016.

Roth, Alvin E.2002. "The Economist as Engineer: Game Theory, Experimentation, and Computation as Tools for Design Economics." Econometrica, 70(4), 1341-78.

Roth, Alvin E.2007. "Repugnance as a Constraint on Markets." Journal of Economic Perspectives, 21(3), 37-58.

Roth, Alvin E.; Tayfun Sönmez and M. Utku Ünver.2004. "Kidney Exchange." Quarterly Journal of Economics, 119(2), 457-88.

Shapley, Lloyd and Herbert Scarf.1974. "On Cores and Indivisibility." Journal of Mathematical Economics, 1(1), 23-37.